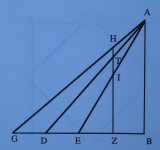
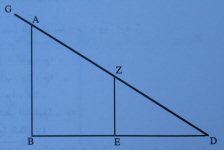
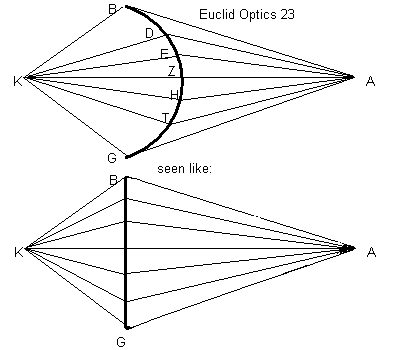
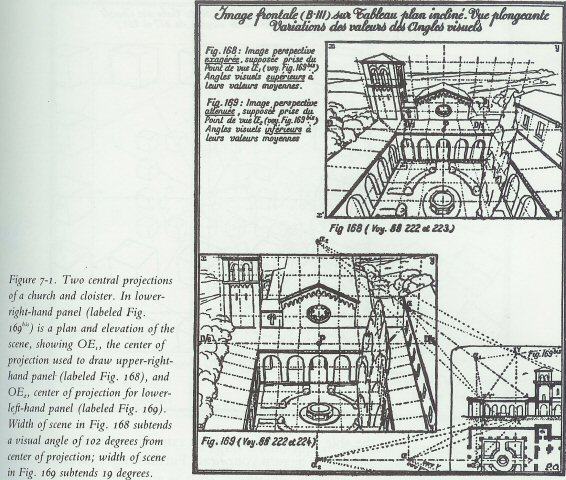
Perspective Seen from Different Points of View

Otto B. Wiersma

17 Feb 2007 – 10 Sept 2007 (last update)

keywords:
depth clues, rectalinear and curvelinear perspective, points of view

Introduction

Plato stated that as things appear, is different from as things are. He found that e.g. perspective (skhnografia - ‘scene-painting’) and the magic of light and shadow often lead to contradictions or illusions. But according to Plato we are rescued from this confusion of contradictions and illusions by measuring, counting and weighting (Republic, X,602C-3B). Aristotle was less afraid to rely on the human senses (resulting in ‘common sense’) while observing the appearance of eventities. It’s after all the human ‘rational sense’ that guides the measuring, counting and weighting. Perhaps already these and for sure later philosophers understood that contradictions and illusions can be involved in the processes of measuring, counting and weighting as well.

An interesting question I like to explore in this sketch is whether the observed ‘appearance’ of eventities (as being different from their supposed ‘reality’) is a matter of social convention or a perceptual necessity.

In this sketch the exploration of this question is focussed on linear perspective.

In the reasoning often pictures (from prehistoric times until today) are used as illustrations of different points of view on linear perspective. In my view the interpretation of these pictures is complicated by the next facts. The pictures most of the time are products of both perceptions and conventions during their time of construction. Also the pictures often are an attempt to attack, to refresh or to renew both perceptions and conventions. And last but not least the actual interpretation of pictures is biased by the present perceptual skills and social conventions of the observer. For instance, taking a rectalinear instead of a curvelinear picture plane as field of representation is a conventional choice, but once this choice is made, geometrical rules hold for the perspectival structures.

It’s good to keep in mind that linear perspective is just one of the many depth clues that are used in our visual system and that can be used (or not) in pictures. For that reason I start my sketch with an overview of the most familiar depth clues.

A strong argument for the conventionality of linear perspective would be the total absence of it in all picture in ancient times. A strong argument for the perceptual necessity of linear perspective would be the presence of linear perspective in at least a substantial amount of pictures of all times. Arguing against the strong conventionality-view of linear perspective, I continue my sketch with an overview of some pictures of different times that among other depth clues also contain at least basic applications of linear perspective.

If specific depth clues are used (or not) in a picture in a specific way, there can be specific conventional reasons for that, like e.g. political motives for the sizes of important figures in Egyptian art, distorsion-correction or religious motives for the reversed perspective in Byzantine art and philosophical relativistic motives for multi-focal linear perspective in postmodernist art. Conventionality in pictorial art can be related also to the balance between symbolic and naturalistic representation. This is the subject of the next section of my sketch: some ‘good’ reasons for ‘bad’ pictures.

Linear perspective implies focal points of view. This topic deals with the properties of focal points of view, both in pictorial art and in philosophy, elaboring the statement of some postmodernists that their point of view is having no point of view (e.g. Ankersmit, 1994).
(..)

Depth clues
monocular depth clues
occlusion (Overlay of contours: If an object A is in front of another object B (but not completely obscuring it), it will interrupt the contours of the object B farthest away from you. As weak clue it indicates only the relative distance.)
object constancy / size gradient (Relative distance can be estimated based on the apparent size of familiar objects. If you know A being smaller or the same size of B, but it appears larger than B, A is perceived as being nearer.)

color vision (Correct interpretation of color, and especially lighting cues, allows the beholder to determine the shape of and distance to objects. For instance light-blue is always interpreted by our brains as representing a far distance compared to red.)

distribution of light and shadow (Sunlight most usually comes from up above, so we tend to infer a lot of depth information based on highlights and shadows. The first image is lighted from above. In the same image, put upside-down, depth appears reversed.)

texture gradient (objects with more detailed, sharper or larger textures are seen as closer)

atmospherical (or aerial) perspective, e.g. fog gradient (due to light scattering objects on greater distance are progressively more obscured by haze)

linear perspective (For example railroad tracks that run parallel, seem to come closer and closer together the farther they are away from you. The converging railroad is an example of the one-point-perspective:)

(the next grids, made by Termes (2007), show more-point grids of rectalinear and curvelinear perspective; imagine the 6^th vanishing point being behind you in a 360 degree view which can be projected on a sphere:)

Thermes artistically explored the optical illusion of ‘being inside the picture’ when looking at that picture on a rotating transparant sphere (perspective-flip from the ‘outside’ sphere to the ‘inside’ image).

motion paralax (If you, while moving, look at two objects, one being closer to you than the other, you'll see the object A, closest to you, moves the most.)
focus / accommodation (The lens of the eye can change its shape to bring an object at different distances into focus. Knowing at what distance the lens is focussed when viewing an object means knowing the approximate distance to that object.)
position relative to the horizon (hight in the visual field: horizon-ratio-relation, by Edgerton (1976) called ‘horizontal line isocephaly’, the heads of more distant persons staying ‘in line’ with the horizon while the feet ‘move up’.)

binocular dept clues
convergence (the relation of the angle between the eyes when they are fixed to an object to the distance of the object, e.g. cross-eyed when the object is very near)

stereopsis (the ability to blend the images of both eyes together; disparity = the slight difference between the images as projected on the two retinas; stereopsis is only effective within the range of a few yards, approx 200 cm)

Several depth clues lead to relative depth values (e.g. occlusion A covers B means that the distance to A < distance to B), other (often combined) clues lead to metrical depth values (the actual distance).

Depth clues in art of all times

Depth clues (including linear perspecive) can be found in ancient art.
Here some examples:

Prehistory
Compare some bisons in Lascaux:

And see the way these animals are pictured in Zalawrouga (Kühn, 1960, p.159,165):

Egypt
oryx picture

aknaton picture

Greek
A lot of scholars argue that the Greek lacked complete knowledge of linear perspective, i.c. the unifying principle of different vanishing points on the eye-line. Most pictures are drawn in profile and front views and not as seen from one point of view. From around 500 BC the dramatic productions asked for rules of perspective to aid the painters of theatrical scenery (skhnografia). Pythagors, Empedicles, Plato and Aristotle discussed physiological and psychological aspects of vision and the nature of light and color. In Physics II,2 Aristotle relates geometry and optics: ‘Optics investigates mathematical lines qua physical’. The Greek architects exercised qualitative optical adjustments (like e.g. entasis in columns) in order to save the appearances. They also compensated for distance, making the more distant parts of sculptures and paintings relatively larger in order to maintain a natural appearance of the whole. Theoretically they were led by the qualitative (subjective) optics of Euclid, who started from assumptions like those stating that visual rays are rectalinear and located and orientated in a visual cone, and based on those assumptions proposed and proves (modo geometrico) theorems like
Magnitudes seen with a larger angle, appear larger.

The more remote parts in planes situated below the eye, appear higher (the projection EF of BC appears higher than the projection DE of AB).

Parallel lengths, seen from a distance, appear not to be equally distant from each other.

According to Theisen (1972, 25) Euclid’s propositions 6,7, 11 ff are closely related to the notion of a vanishing point or line.

With perceptive observation and ‘rules’ like this in mind, greek artists could produce pictures like the next examples, showing fragmentary linear perspective.

Mind the chair and its legs:

Mind the open door:

Mind the examples of orthogonal perspective-lines in several objects:

Romans

Several Pompei wallpaintings show the fragmentary use of linear perspective:

Lucretius

Diomede (mind the ‘fishbone’-perspective)

Laestrygonians fresco in Roman domus

Room of the Masks (Rome, 1^st century BC) with a central vanishing point

Paris Psalter (10^th century)

Iraq/Persia
Al-Farabi (870-950) extended Euclid’s qualitative (subjective) optics with quantitative (measuring) optics, which was later extended by Alhazen, who argued that the visual angles are not the sole factor in the perception of apparent size, but that the proportions of objects follow the proportions of distance.
Abu Ali al-Hasan ibn al-Haytham (965 – 1039), also known as Alhazen, wrote Kitab al-Manazir (Book of Optics), showing that light is reflected from an object into the eye contrary to the idea of some ancients [e.g. the Pythagoreans] that vision is an active process, the eye sending out beams itself. [Alhazen adapted the ancient approaches of the Epicureans (the eye receives impressions from the object) and Democritus (object > images in the air > transmitted to the eye)] He is, among a lot of other scientific achievements, also seen as giving optics (and thereby indirectly also the geometry of perspective) the turn of experimentally controled postulation.

Italy
Giotto (1289) townview
Lorenzetti (1340) townview
Brunelleschi (1377–1446) was with his graphical experiments the first systematic painter of compositions in which the linear perspective dominated the scenes.
Leon Battista Alberti (1404-1472) has been credited with the first written account of a comprehensive theory of linear perspective in 1435 (De Pictura), with which he wanted to instruct the painter how he can represent with his hand what he has conceived with his mind (sc the related mathematics).

According to Crombie (1996,106) the exact measurement and true scaling required by linear perspective completely transformed the communication of information in the sciences and technical arts through picturial illustrations. (..) Depiction became an instrument of scientific research.
(..)

Some ‘good’ reasons for ‘bad’ pictures

(..)

Focal points of view

(..)

Conclusion

(..)

Links to places on this page where you can find abstracts of / about

Andersen, K., The Geometry of an Art. The History of the Mathematical Theory of Perspective from Alberti to Monge, 2007
Boorstin, D.J., The Discoverers. 1983
Collier, J.M. Linear Perspective in Flemish paintings and the art of Petrus Christus and Dirk Bouts, 1975
Davies, M., Turner as professor: the artist and linear perspective, 1992
Derksen, A.A., Linear Perspective as a Realist Constraint. Journal of Philosophy, CII(5), 235-258, 2005
Edgerton, S.Y., The Renaissance Rediscovery of Linear Perspective, 1976
Kheirandish, E., The Arabic Version of Euclid’s Optics (2 Volumes), 1999
Kubovy, M., The Psychology of Perspective and Renaissance Art, 1986
Richter, G.M.A., Perspective in Greek and Roman Art, 1970
Termes, D., New Perspective Systems, 2007
Theissen, W.R., The medieval tradition of Euclid’s Optics, 1971
$$$

Links naar abstracts in het Nederlands

Berg., J.H., Metabletica van de Materie I, Meetkundige Beschouwingen, 1968

Literature

Andersen, K., The Geometry of an Art. The History of the Mathematical Theory of Perspective from Alberti to Monge, 2007
Ankersmit, F.R., History and tropology: the rise and fall of metaphor, 1994
Arnheim, R., Art and visual perception: A psychology of the creative eye; the new version, 1974
Boorstin, D.J., The Discoverers. 1983
Brownson, C.D., Euclid’s Optics and its Compatibility with Linear Perspective, in Archive for History of Exact Sciences, 24, 165-194
Cassirer, E., The Philosophy of Symbolic Forms, 1955
Collier, J.M. Linear Perspective in Flemish paintings and the art of Petrus Christus and Dirk Bouts, 1975
Crombie, A.C., Science, Art and Nature in Medieval and Modern Thought, 1996
Davies, M., Turner as professor: the artist and linear perspective, 1992
Derksen, A.A., Discovery of Linear Perspective and its Limitations. Philosophica 63(1), 19-50, 1999
Derksen, A.A., Linear perspective as a realist constraint: a case against Goodman's and postmodern conventionalism. University of Calgory, Canada, Lecture philosophy department and philosophy of art students, 1999
Derksen, A.A., Lineair perspectief als remedie tegen pragmatisme, conventionalisme, relativisme en andere kwalen. ANTW 93(4), 274-291, 2001
Derksen, A.A., Occlusion shapes and sizes in a theory of depiction: merits and demerits. British Journal of Aesthetics, 44 (4), 319-341, 2004
Derksen, A.A., Pitfalls of pictorial space. In J.J. Graafland & F. van Peperstraten (Eds.), De omheining doorbroken. Economie en filosofie in beweging (pp. 213-224), 2004
Derksen, A.A., Linear Perspective as a Realist Constraint. Journal of Philosophy, CII(5), 235-258, 2005
Doesschate, G. ten., Perspective – Fundamentals, Controversials, History, 1964
Edgerton, S.Y., The Heritage of Giotto’s Geometry: Art and Science on the Eve of Scientific Revolution, 1991
Edgerton, S.Y., The Renaissance Rediscovery of Linear Perspective, 1976
Euclid, The Arabic Version of Euclid’s Optics, edited and translated with historical introduction and commentary [by] Elaheh Kheirandish,1999
Field, J.V., The Invention of Infinity. Mathematics and Art in the Renaissance, 1997
Gablik, S. Progress in Art, 1976
Gibson, J.J., The Information Available in Pictures, Leonardo 4, 1971
Gombrich, E.H., Art and Illusion: a Study in the Psychology of Pictorial Representation, 1960 / 1969
Gombrich, E.H., Image and code: scope and limits of conventionalism in pictorial representations, in: The image and the eye: further studies in the psychology of pictorial representation, 1982
Goodman, N., Languages of Art: an Approach to a Theory of Symbols, 1968 / 1976 [relativistic conventionalism of linear perspective]
Jammer, M., Concepts of Space: The History of the Theories of Space in Physics, 1969
Kepes, G., Language of Vision, 1944
Kheirandish, E., The Arabic Version of Euclid’s Optics (2 Volumes), 1999
Kubovy, M., The psychology of Perspective and Renaissance Art, 1986
Kühn, H., Prehistorische Kunst in Europa, 1960
Little, A.M.G., Perspective and Scene Painting, Art Bulletin 1937, vol 19, 487-495
Mikocki, T., La Perspective dans l’Art Romain, 1990
Olmer, Perspective Artistique, 1943,1949
Panofsky, E., Die Perspektive als symbolische Form, Vorträge der Bibliothek Warburg, 1924-1925, 1927 pp 258-331 [influenced by Ernst Cassirer]
Pirenne, M.H., Vision and the Eye, 1948
Pirenne, M.H., The Scientific Basis for Leonardi da Vinci’s Theory of Perspective, in The British Journal for the Philosophy of Science 3, pp 169-185, 1952-1953
Richter, G.K., A Handbook of Greek Art, 1965
Richter, G.M.A., Perspective in Greek and Roman Art, 1970
Termes, D., New Perspective Systems, 2007
Theissen, W.R., The medieval tradition of Euclid’s Optics, 1971
Veltman, K.H., Linear Perspective and the Visual Dimensions of Science and Art, 1986
Welch, R.B., Perceptual modification: adapting to altered sensory environments, 1978
White, J. Perspective in Ancient Drawing and Painting, 1956

Sites
Optical Illusions:
scientificpsychic.com
michaelbach.de
ritsumei.ac.jp
depth clues, e.g.:
http://www-psych.stanford.edu/~lera/psych115s/notes/lecture8/
curvelinear perspective optical illusions, e.g.:
http://www.termespheres.com/qt-directory.html

Artificial Memory

Abstracts in English
From Richter, 1970 and Andersen, 2007.
Literary evidence for ancient understanding of perspective?
Plato (428-348 BC) Sophist, 236A, describes how, in some large sculptures and paintings, objects are not reproduced in their true proportions, because this would make the upper parts seem too small.
Euclid (around 300 BC), Optics (KA: E’s theory accounts for visual appearances and not for projections).
Angle Axiom: Magnitudes seen within a larger angle appear larger, whereas those seen within a smaller angle appear smaller, and those seen within equal angles appear to be equal.
Theorem 4 When objects are situated along the same straight line at equal intervals, those seen at the farther distance appear smaller.
Theorem 5 The appearance of objects of the same size which are placed in different locations appear different, and those which are nearer to the eye appear larger.
Theorem 6 Parallel lengths [magnitudes], seen from a distance, appear not to be equally distant from each other.
[KA calls this the convergence theorem and states that this optical result is not compatible with the theory of perspective. Euclid argued that the visual angles become smaller for more distant line segments, which is only valid if the point of view lies between the two parallel lines. See:]

[OBW but taken into account Euclid’s 7^th proposition seems to meet this objection – see below]
[Despite the difference between optics and perspective (cf also Panofsky, 1927 (incompatible) and Brownson, 1981 (compatible)), KA states that it’s quite possible that the convergence theorem inspired some drawers in antiquity and other drawers during the Renaissance to depict orthogonals as converging lines (2007,726)]
Theorem 8 The appearance of equal and parallel magnitudes, when placed at unequal intervals from the eye, is not in proportion to the distances.
Theorem 10 Of planes lying below the eye, the farther parts appear higher.
[KA calls this the remoteness theorem]

Theorem 11 Of planes lying above the eye, the farther parts appear lower.
Theorem 12 Of lines which extend forward, those on the right seem to swerve to the left, and those on the left to the right.
Vitruvius (1^st Century BC), De architectura 1.2.2 In like manner scainography (i.e. perspective) is the method of sketching a front with the sides withdrawing into the background, the lines all meeting in the centre of a circle (item scaenographia est frontis et laterum abscendentium adumbratio ad circinique centrum omnium linearum responsus) and in 7, preface 11: (.) given a central point the lines should correspond as they do in nature to the point of sight and the projection of the visual rays (. > ) clear representation of the appearance of buildings in painted scenery (.) (ad aciem oculorum radiorumque extentionem certo loco centro constituto, ad lineas ratione naturali respondere, uti de incerta re certae imagines aedificiorum in scaenarum picturis redderent speciem).
Lucretius (1^st Century BC), De rerum natura, 4,426 collonade as a narrowing cone, right and left side brought together into the dim apex of a cone (donec in obscurum coni conduxit acumen), cf Seneca De beneficiis, 7,1,5.
Geminus (1^st Century BC): convergence of parallel lines as illusion in the perception of objects at a distance (from Proclus’ commentary on Euclid’s Elements).
Proclus (412-485) On Eulcid, 1,40.10: the apparent convergence of parallel lines
Richter: The greek word skhnografia (scene painting) related perspective to the theatre, where every person in the audience furnished a different point of sight, so the desirability of unifying a picture from a single point of view was not so obvious. [OBW also the different personae on stage represented different points of view]
OBW Linear perspective was partly understood by the ancient mathematicians but hardly practiced by the ancient artists, who (if at all) most of the time used different points of convergence for different planes. Only from the Renaissance on the fragmentary ideas became worked out into geometrical and algebraic theories, involving complete sets of postulates, theorems and proofs while the artists by that time tried to put everything in the right perspective of one consistent point of view. Renaissance was the time in which rational arguments (as inheritence from the anciencts) joined with rational measurements and calculations (as formalized by algebraic functions).

In the Netherlands around 1600 several artists and mathematicians studied and practiced linear perspective.

Hans Vredeman de Vries (1527-1607), artist

Simon Stevin (1548-1620) served Maurits and wrote ‘Van de Deursichtighe / Van de Verschaeuwing (1605) in which he also extended the Dutch language with new technical terms like deursichtighe (perspective), verschaeuwing (scenographia), saempunt (vanishing point), spiegelschauwen (catoptrics) and wanschaeuwing (refraction), meetconst and wisconst. In his book one can find also the hint to look at a picture through a small hole in order to gain the best impression of naturalistic perspective.

Samuel Marolois (c 1572 – c 1627) fled with his protestant father from France to the Netherlands where he also served Maurits. He became one of the most read Dutch perspectivists with his ‘La Perspective contenant la theorie et la practique d’icelle’ (1614), not least due to its vivid and instructive illustrations.
His book was by that time translated into Latin, Dutch and German.

The next staircase perspective of Marolois perhaps inspired Rembrandt and Salomon Koninck, although they worked out an even more complicated spiral-cored staircase.

Andersen (2007) summarizes the next three major steps in the theoretical development of linear perspective since Renaissance:

Guidobaldo Del Monte (1545-1607): the vanishing point theorem (The perspective image l_i of a line l that is not parallel to the plane p passes through the vanishing point V_i of line l and so do the perspective images of all lines parallel to line l.)

Brook Taylor (1685-1731): generalized concept of the vanishing line ( The image l_i of any line l that is not parallel to the picture plane p, is determined by the vanishing point V_i and the intersection I_l.)

Johann Heinrich Lambert (1728-1777): abstract perspective geometry. Anlage zur Perspektive, 1752; Die Freye Perspektive, 1758.

Andersen gives a nice piece of reasoning of Lambert:

[OBW:
If the Lambert-picture is redrawn in perspective (appropriate to the subject) it would look like this:

And an extension of this picture very nicely shows how the projections (the thick blue and the thick red line) of two parallel lines l1 and l2 onto the plane p end in a joined vanishing point V on the eye-line of observer O in the plane p.

This picture also represents simultaniously two different points of view: we are from our point of view (which could be reconstructed while applying reverse projection) observing the observer O and we are looking at what O sees in the picture plane p when O is looking at the lines l1 and l2. Through PV
runs the vanishing line (eye-line) of O and our vanishing line is the horizontal line at the top of the picture.

Apart from the elgancy of his geometric demonstration of vanishing line and vanishing points, something in Lambert’s reasoning does not seem to make sense and in my view that’s the bit ‘infinity’ involved in it.
If moving A into infinity would make FC parallel to the line l and coincide with FB and OA would coincide with OV, this would mean that point A would be simultaneously on the three parallel lines (l (QA), OV and FB). It would also seem to imply that when one enlarges a triangle long enough, it will become a square, which would be somewhat contradictive.
We have to mind that in Lambert’s argument only B moves into ‘infinity’, while C is fixed. If B moves to a large distance, the line BD will approach CD, but only at the present limited range of CD.

In the figure of Lambert the issue is the effect of the movement of A in the plane p, sc the effect that A_i. will approach V. And this issue should focus on appearance (sc what happens in the plane p) related to a large distance of A, for which ‘infinity’ seems not to be a necessary or helpful concept. The question of appearance should be: if A moves, what is the distance QA at which the human eye can no longer distinguish the difference of A_Iand V in the plane p.
Now every successive doubling of the length QA reduces the distance A_IV by half, so when the human eye can no longer distinguish A_I and V we find the factual vanishing point A that’s related to the plane vanishing point V, seen from O (the position of the eye). Moving A further than the factual vanishing point does not add any information to what can be seen on the plane p.

The position of the factual vanishing point A depends on the position of O : its heigth and and its distance to the plane p. Suppose the distance between A_I and V has to be < 0.1 mm (as arbitrary example-measure) in order to be no longer visible to the human eye, and suppose we vary the position of O, we can construct the next table.

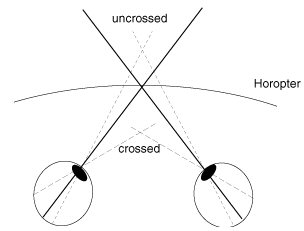
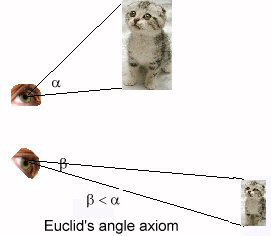
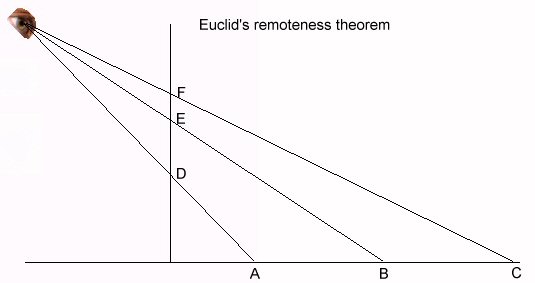
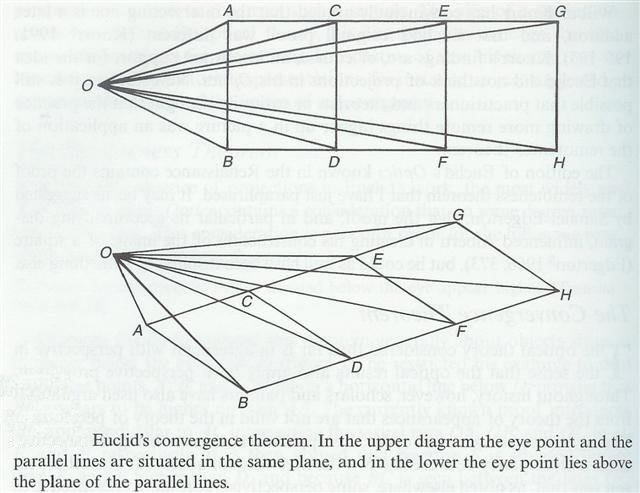
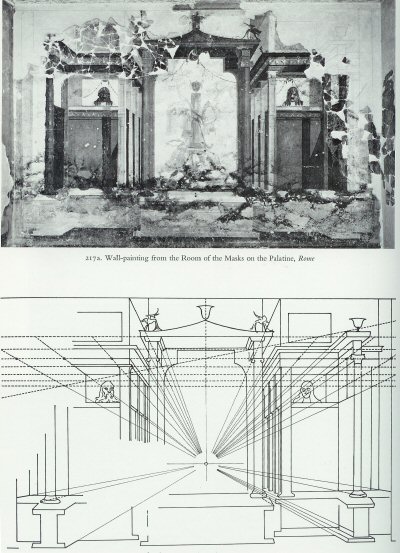
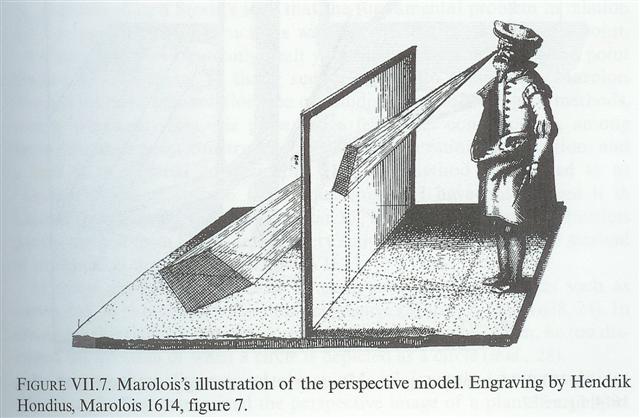
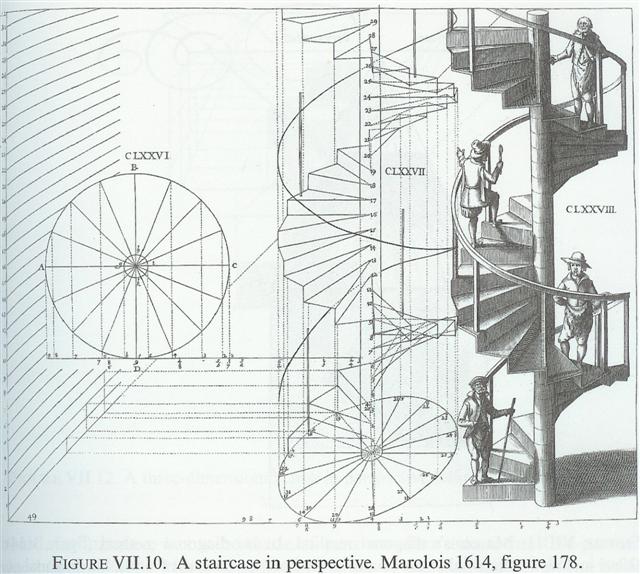
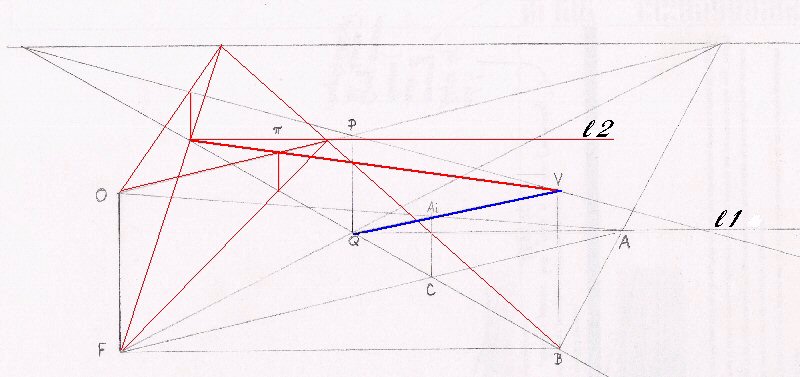
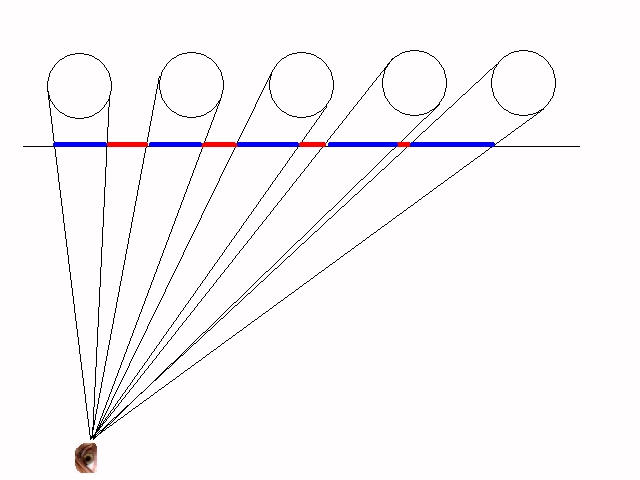
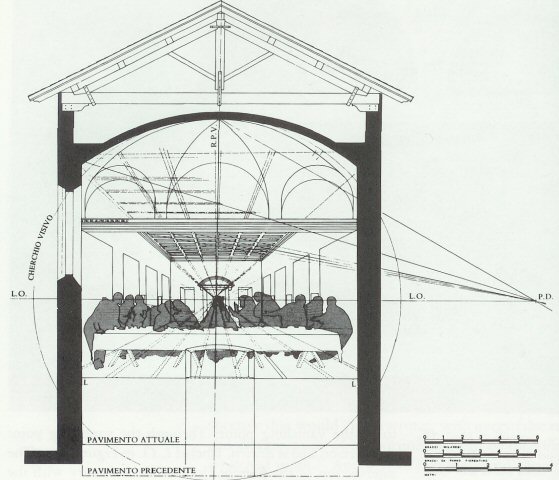
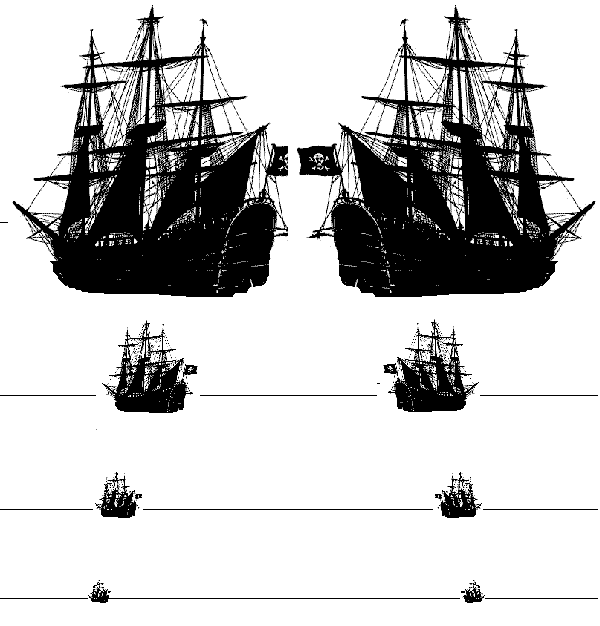
eye-hight & plane-distance of O	number of steps to reduce the distance between A_I and V	resulting distance QA
1 cm	7	1.28 m
10 cm	10	102,4 m
1 m	14	16.384 km
2 m	15	65.536 km

Infinity does not come into the picture.]

Boorstin, D.J., The Discoverers. 1983
Seeing the Invisible (pp 293ff).
For long it was thought that the bigger and smaller world were not only unknown, but also of different order. If that would be correct, than it would not be allowed or even possible to unify its representations into one framework. This view changed with the invention of novel instruments like the telescope and the microscope, which implied the next developments: see and hear with the God-given senses > disputes about what was seen with the naked eye > use of technical instruments > disputes about what was seen with those instruments > > how to interpret what was seen with the instruments > completely different framework of thought (moving from the Aristotelian-Ptolemaic universe to the Copernican-Galilean universe and the universe of the very small (e.g. Leeuwenhoek’s animalcules [bacteria]) > the big and the small are not of completely different order, but of the same order [sc mechanics and laws].
294 science’s paradox: things [in science] are no longer what they seem [for common sense].
Egypt: myth of the sun moving around the earth (sungod Ra)
Greek: earth as sphere, heavens as rotating spherical dome (two-sphere universe)
Pythagoreans: knowledge above the data of human senses, mathematics as the only way to the truth
Plato: geometry more real than physics (>neoplatonists like Proclus)
Aristotle: 55 etherial shells, describing the heavens as they looked
Renaissance: reborn neoplatonism vs scholasticism (sc Aristotle’s hardheaded common-sense approach)
Copernicus (1473-1543) did not change the system, but the location [& movements] of the bodies; easthetic concern: he thought his scheme to be much more simple & beautiful (De Revolutionibus Orbium Caelestium, 1543)
Tycho Brahe (1546-1601) found a lot of new stars (up till 1000)
Kepler (1541-1630) saw the sun as a center of force, replacing the metaphysical concept anima/soul (the ‘anima motrix’, the moving spirit of each planet) by the physical concept ‘force’. His 3 laws of planetary motion could be regarded as the start of modern physics, e.g. the greater the distance from the sun, the weaker the force of the sun (311).
312 The leap from the naked-eye vision to instrument-aided observation counteracted the prejudices of the faith in the unaided, unmediated human senses, although mirrors, prisms and lenses at first did not provide very clear images (which is the reason why they by that time often were seen as devices for making visual lies, distorting the truth, trickery). 313 There were also religious obstacles: God=Light, 1^st day of creation: let there be light – not something to fool around with using unreliable instruments. In practice it nevertheless helped that putting eye-glases on their nose considerably enhanced the vision of scientists with visual problems. So the simple and practicle eye-glases stood at the start of a revolution that lead to seeing the invisible, first of all by the telescope.
314 Around 1600 the Dutch spectacle-maker Hans Lippershey in Middelburg did put two lenses together and discovered that this combation provided a considerable enlargement of the image. In 1608 he did send a petition to the States General ‘for making these instruments for the unility of this country alone’, while The Netherlands were battling for indepencence against the well-financed armies of Philip II of Spain. A committee of the Dutch commander Maurits of Nassau declared it ‘likely to be of utility to the State’. But because of other inventors and imitators the exclusiveness of the use of the telescopes was not secured. 315 Under the name of ‘Dutch trunks’, ‘perspectives’ or ‘cylinders’ they appeared all over Europe and also reached Galileo (1564-1642). The natural philosophers by the time of Galileo’s observations were reluctant to see through his telescopes, e.g. reporting ‘below it works wonderfully, but in the sky it deceives one, as some fixed stars are seen double (..) excellent men and noble doctors have admitted the instrument to deceive.’ (316). For years Galileo kept on improving and testing his instruments and observations, crusading for the paradoxes of science against the tyranny of common sense, which would have a big impact on the way scientist and laymen changed their way of thinking, cf the next poem by John Donne (1572?-1631):

And new Philosophy calls all in doubt,
The Element of fire is quite put out;
The Sun is lost, and th’earth, and no mans wit
Can well direct him where to look for it.
And freely men confesse that this world’s spent,
When in the Planets, and the Firnament
They seeke so many new; then see that this
Is crumbled out againe to his Atomies.
‘T is all in peeces, all cohearence gone;
All just supply, and all Relation…
and in these Constellations then arise
New starres, and old do vanish from our eyes…

317 The experimental spirit by the time of Galileo was inspired by military and commercial enterprises. Galileo was professor of mathematics af Padua and did run a shop for making surveying instruments, compasses and other mathematical apparatus in order to supplement for the meager honorarium as professor. 318 In 1609 a three-power telescope [from the Netherlands?] was demonstrated in Padua and Venice. Galileo took over and improved the ideas in making first a nine-power and later that year a thirty-power telescope, using a plano-convex objective and a plano-concave eyepiece. In 1610 Galileo turned his telescope toward the skies, penetrating the majesty of the celestial spheres. He published what he saw in ‘Sidereus Nuncium’ (The Starry Messenger) nd reported having seen starts in myriads, the surface of the moon being rough and uneven just like the surface of the earth itself, settling disputes about the Galaxy and the Milky Way – appearing to be a mass of innumerable stars planted together in clusters. He also reported having seen four new planets: the satellites of Jupiter. Each observation shook another pillar of the Aristotelian-Ptolemaic universe, so G announced his sympathy for the Copernican system. 321 G moved to Florence where his observations began to provide direct evidence of a heliocentric system. In 1611 he triumphed in Rome, where some of the Church authorities looked trough his telescope and enjoyed what they saw, but still did not accept Galileo’s interpretation. 322 At a banquet of the pioneer scientific society ‘Academia dei Lincei’ in Rome Galileo’s instrument was christened ‘telescope’ as suggested by a Greek poet-theologian who happened to be present. And so began the custom to give instruments of modern science names borrowed from ancient Greece. Back in Florence G tried to defend the simultaneous truth of the Bible and the Copernican theory, stating about the language of the Bible and the language of Nature: ‘two truths never contradict each other’. 323 But cardinal Bellarmine sniffed heresy, having common sense on his side: man’s everyday experience tells him plainly that the earth is standing still, thereby also taking the Scripture’s literal meaning as correct. Galileo made the mistake to go to Rome and try to convince pope Paul V and cardinal Bellarmine that the earth moved, which idea was condemned. Duhem and Popper argued that in the light of modern positivism Bellarmine was closer to the truth than Galileo, who had not explained what really happens, while Bellarmine recognized that the Copernican theory merely ‘saved the appearences’. 324 In 1632 [OBW the year of Rembrandt’s ‘méditation visionnaire’] Galileo published his ‘Dialogue on the Two Chief World Systems’, debating the geocentric and heliocentric theories. To reach a lay audience as well, he offered his work not in Latin, but in Italian. 325 In 1633 the Pope forbid the Dialogue and Galileo was to make public and formal abjuration and to be imprissoned for an indefinite period. 326 So Galileo, being 70 years old, was forced to state: ‘I must altogether abandon the false opinion that the sun is the center of the world and immobile and that the earth is not the center of the world and moves (..) the said doctrine was contrary to Holy Scripture.’ In Florence under house-arrest he wrote a book on ‘two new sciences’, one concerned with mechanics and the other with the strength of materials. This book was smuggled out of the country and printed by the Elzevirs af Leyden in The Netherlands.
327 The microscope was a product of the same age that made the telescope. The leading candidate for inventing the microscope is Zacharias Jansen, an obscure spectacle-maker in Middelburg, The Netherlands. In the beginning the word ‘perspicillum’ was used for both telescope and microscope. Galileo reported in 1614 seeing flies look as big as lambs using a microsopic device. 328 John Faber (1574-1629) came up with the name ‘microscope’ for the instrument. The suspicions of ‘optical illusions’ was enhanced by the chromatic and spherical aberrations of the microscopes that produces fuzzy images. In 1665 Robert Hooke (1635-1723) published ‘Micrographis’ with 57 amazing illustrations. The most prominent microscopist by that tiime was Antonie van Leeuwenhoek (1632-1723). 329 Although there was vehement military and commercial rivalry between the Dutch and the British, at the same time there was vigorous collaboration in science, exchanging information and sharing new scientific vistas. 330 Leeuwenhoek ground some 550 lenses of which the best had a linear magnifying power of 500 and a resolving power of one-millionth of a meter. The Royal Society encouraged Leeuwenhoek to report his findings in 199 letters. Using his microscopes L was excited to discover a universe in every drop of water. So he reported in 1674 seeing very small animalcules [sc bacteria], each several creature having its own proper motion. 331 L persuaded the Royal Society of his findings by providing testimonials of respected eyewitnesses (‘testis oculatus’), who had seen the little animals with their very own eyes. 332 L opened vistas into microbiology, embryology, histology, entomology, botany and crystallography. He was elected Fellow of the Royal Society in 1680.

Collier, J.M. Linear Perspective in Flemish paintings and the art of Petrus Christus and Dirk Bouts, 1975
11 Ancient art was centered on individual objects with little emphasis on spacial relations. (..) The human forms were usually made up of a multitude of vieuwpoints (..) fragmented spatial organization.
13 What can be found of theory of perspective and examples of perspective in the work of the Greek and the Romans? According to Collier E. Panofsky found no adequate perceptive theory and no pictorial examples, J. White found theory but no examples, G. Richter found examples but no theory and D. Gioseffi (‘Perspective’ in Encyclopedia of World Art XI, 1960, p 198) found both theory and pictorial evidence.
14 Most Roman painting showed fragmented spatial organization with multiple viewpoints. (..) Medieval perspective generally used spacial elements as surface patterns on the picture plane – abstraction of the forms of ancient art > development of rational pictorial space, desire for a more representational / naturalistic approach.
15 14^th cent. Cavallini, Giotto: converging sides (work of 1290, 1305)
29 Jean Fouquet and Leonardo da Vinci: curvelinear or synthetic perspective systems. 30 Leonardo da Vinci: planar perspective seems not to respect the proportionality between the distance of on object and its apparent size, see e.g. the diagrams on p 311:

40 Most 15^th cent. artists were striving primarely to find simple techniques for making workable perceptive pictures.

Davies, M., Turner as professor: the artist and linear perspective, 1992
In 1807 Turner was elected professor of perspective.
41 standard perspective (representation from a single point of view with mathematical accuracy of an object on a plane) and vision (the ‘true appearance’ of that object) are different.
43 Turner: there should be a ‘ joined coincidence’ between [perspective] rules and nature [natural vision] (..) rules are the means, nature the end (Lecture 2).
As artist Turner seemed to have problems in consistently regulating vertical convergence, which can be seen in his picture St George’s Bloomsbury. See e.g. the sides of the tower in this pictures:

82 standard perspective is dominated by straight lines (rectalinearity), but in vision one finds curvelinearity and in nature lots of irregular curved forms, so Turner stated that standard perspective is too straight (83)
90 Thorough knowledge of perspective gave artists (like Turner) the ability to manipulate the viewpoints from which they showed objects in their pictures.
By curving the foreground architecture Turner broke the window of standard perspective to allow the viewer to enter the picture space:

98/99 Turner, taking into account the elliptical shape of the visual field, sometimes exhibited his paintings with covered corners. Sometimes he painted the corners of the square pictures with curving brushstrokes. 100 And he also made ‘vignettes’: circular scenes fading out towards the edges, representing peripheral vision.

Derksen, A.A., Linear Perspective as a Realist Constraint. Journal of Philosophy, CII(5), 235-258, 2005
Derksen takes linear perspective as a stand against pragmatism, relativism, postmodernist conventionalism ‘and other diseases’ (ANTW 93(4)).
Contrary to the Chinese parallel perspective and the Byzantin reverse perspective, linear perspective provides a more ‘faithful’, convincing image: the pictorial space in a linear-perspective picture is experienced as (closely) resembling the depicted world (235). D’s main argument is the need of linear perspective to counteract the working of size constancy within the pictorial space (Size Constancy Argument). The next pictures (from different articles of D) show the way size constancy works in relation to linear perspective:

According to D linear perspective is required for a convincing pictorial space due to some features of our perceptual apparatus (241) Objective features of the human perceputal apparatus determine the visual field of the observer (251). D refers to different psychological experiments in which seeing virtual space (sc a picture) or seeing real space did make no significant difference for adequate action (throwing balls or judging depth), from which he concludes that linear perspective is the single most important factor (Depth Argument). There are still significant personal differences in judging size constancy, occlusion sizes and depths. Because of this flexibility of our perceptions, and e.g. because elements which are shown correctly according to linear perspective, nevertheless in too close pictures are experienced as distorted (see picture below), D’s main argument boils down to a ‘Weak Size Constancy Argument’.

Edgerton, S.Y., The Renaissance Rediscovery of Linear Perspective, 1976
short timeline:
300 BC Euclid Optics
175 AD Galen: physiological structure of the eye: lens
140 AD Ptolemy, Optica: centric visual ray; Geographica: linear perspective construction for drawing a worldmap.
1000 AD Alhazen: integration Euclid, Ptolemy and Galen
1260 Roger Bacon, Optics
1270 John Pecham, Perspectiva communis
1390 Basius of Parma, Questiones perspectivae
1400 Ptolemy’s Geographica in Florence
1420 Toscanelli (friend of Brunelleschi and Alberti) Della prospettiva
1425 Brunelleschi, linear perspective pictures
1435 Alberti, Treatise on painting / perspective
Geometrical linear perspective is different from ‘perspectiva artificialis’ (what can be seen from different points of view – reverse perspective, split-view).
6 Is linear perspective a discovery [perceptual necessity] or an invention [convention]? The picture as framework window as rather a specific notion [OBW rectalinear picture plane as ‘field of representation’ a conventional choice?].
12 J.J. Gibson: difference between the complementary visual world (experienced, moving around, connected with other senses, providing more information about the nature of objects, leading to depth shapes) and visual field (fixating the viewpoint, providing more information about relative sizes, locations and relations of objects, leading to projected shapes).
See e.g. the next Byzantin picture:

E: In this Byzantin picture the reverse perspective depicts what is experienced in the visual world [OBW specific details show what can be seen from different viewpoints – pre-holographic? Perspective in this picture is not consistently reversed but mixed, compare the upper part of the picture. It seems that only a significant element of this picture has been drawn in reverse perspective.]
14 It is natural to be begin making pictures in this way [sc reverse perspective, split-view], cf children en other cultures [OBW but then one would expect this to appear consistently in their pictures, which is not the case]
16 Around 1260 Roger Bacan stated in his Optics that painters should become skilled in geometry – with this knowledge they could ‘make literal the spiritual sense [sc of biblical truths]’. E. regards this statement as a key to understanding the evolution of western realism.
19 In 1277 the bishop of Paris banned Aristotle because he described the universe as finite. E: This ban cleared the road for taking space as infinite and homogeneous and the advent of linear perspective.
20 13?? Thomas Bradwardine of Canterbury saw God as infinite sphere, whose center is everywhere and whose circumference is nowhere.
Middle Ages: subjective view of the world – each element separate and independent [OBW naïve holographic representation – as seen from different points of view], 21 Middle Ages absorbed within the visual world (Gibson).
But Renaissance: a removed viewpoint, [spacially uniting different elements].
22 psychological development of the sense of space (e.g. before 8 years non-perspectival, after 8 an understanding of space structuration): every stage valid, autonomous and complete, 23 related to the change of the internal structuring processes of the mind itself.
24 E: the Renaissance perspectival constructions were not only intended to objectify the physical environment, but also to enhance the allegorical, moral and mystical message in the scripture and the lifes of the saints > pictures as examples for the moral order and human perfection.
25 In geometry textbooks until 1500 a cylinder figure was represented by parallel sides and equal circles on each end (a), later suggusting depth with shading (b):

E: Brunelleschi / Alberti rediscovered the vanishing point – convergence of parallel lines at an infinite [?OBW] point on the horizon, 26 grasping the geometrical and optical principles by which this appears to happen. E: before Brunelleschi no one elucidated this phenomenon in ordinary sight, much less in pictures [OBW but compare e.g. picture in Pompei and Rome BC]. Alberti: the ‘centric point’ as single locus for all converging architectural lines, ‘distance point’ as geometrical constructing to be able to draw the deminishing depth of pictorial elements, E: ‘horizontal line isocephaly’ (of people at various distances the heads are seen as staying on the horizon, while the feet rise up).
27 Trinity (1425) of Masaccio is an early Renaissance example of the one point perspective:

30 Brunelleschi had a pragmatric outlook and artistical competence, Alberti studied linear perspective in theoretical terms as unifying pictorial space [optical space of the visual world– unification of vision before the unification of the representation in a visual field], building a world of order and real space functioning according to geometrical laws as service to ‘istoria’ (history painting).
31 perspective as visual metaphore of the superior existence of ‘virtu’, ‘onore’ and ‘nobilita’ [sc in ‘istoria’], a compelling model, based on classical ideals and geometric harmony.
36 Florence around 1400: interest in the practical application of arithmetic and geometry in all walks of the city’s life – mathematics as the lingua franca, ability to measure as the root of all wisdom (Nicolaus Cusanus’ Idiota).
37 The need for trained clerks and accountants > schooling lower classes, artisan/engeneers designing buildings, fortifications, weapons, waterworks and machinery of all kinds – requiring skills in mathematics and the ability to draw complex mechanical devices with convicing illusion of three dimensions.
43 Alberti’s ‘centric point’: ‘lines to an almost [OBW sic!] infinite distance’ (Alberti, De Pictura, pg 54,55)
43-47 relation vanishing point V (=Alberti’s ‘centric point’) and distance point D, together with the variable intersection-line l used in a geometrical method for determining the foreshortening of e.g. square tiles:

44 E states that ‘horizontal line isocephaly’ is not seen in pictures before 1425 [OBW look for the black swan, e.g. the Zalawrouga-pictures].
55ff In Renaissance not one viewpoint, not just an abstract arrangement of lines and shapes as ‘goal’, not aesthetics (an 18^th century concept), but the desire to infuse geometric (divine) harmony into the pictures, primacy of objective physical and metaphysical realism, showing God’s geometrically ordered universe, over artistic subjectivity. Linear perspective as servant, not as master. Compare e.g. Domenico Veneziano’s ‘Madonna and Child Enthroned with Standing Saints’ (1445), in which the architecture ‘embraces’ the figures, with Edgerton’s more geometrically correct reconstruction which places the horizontal line at head level, but detaches the architecture from the figures.

59 The priority of the moral and philosophical ideas of a civilization can be reason for not applying Alberti’s perspective rules. 60 The geometric concept of light-filled space provided some kind of rationalization of how God’s grace pervaded the universe.
61 Pado dal Pozzo Toscanelli (1397-1482), influential friend of Brunelleschi and Alberti.
65 Greek Optics as only stepfather of geometrical perspective (theory) and artificial linear perspective (the illusionary visual effects in pictures). In perspectiva a combination of Greco, Roman, Arab and Middle-Age-Christian scholarship > tendency to ‘see’ the natural world according to Euclidian (geometric) rules.
66 The old philosophers were not concerned with pictures [?OBW the problems of representation?], but with issues as the force of vision (into or from the eyes), the relation of visual rays (space in between?), the primary role of the surface or the inner nerve of the eye, how the image was processed and complexities of binocular vision. 67 ancient Greek optics as a physical explanation of seeing.
Different approaches:

atomists: objects > eidola (picturelike effluxes) > trough the air > exact image in the eye; Epicurus: intromission theory of vision
pythagoreans: camel too big to enter the eye – vision from the eye: extromission theory of vision; Stoics: visual force from the eye, form of the visual cone: apex in the eye, base at the object
Plato: combination extromission (‘fire’ emitted by the eye) and intromission (force by the objects), a touching of forces, transmitting back the sensation of sight to the eyes
Aristotle: objects activate a medium (e.g. air or water) when light is present – this is sensed by the eyes, which project a receiving force from the ‘soul’ (sc cognitive center of the brain) – no vision in a void

68 Euclid (4^th c. BC) Optics: a geometrical model for optics (still not concerned with the problems of pictures), Ptolemy (2^nd c. BC) Optics, again more physical (e.g. color, atmospheric perspective), centric visual ray principle, Galen ( ): anatomy of the eye (lens, vitreous humor, optic nerve)
70 scenographia: theatrical scene painting, 71 some kind of vanishing point system for painting stage backdrops (cf Vitruvius in ‘De Architectura’, 1^st c. BC: ‘correspondence of all lines to the centre of a circle’), 72 Greek > Arab translations of Al Kindi (9^th c. AD), De Aspectibus, De Radiis; Avicenna (‘eye-lens acting as a mirror’) and Alhazen (11^th c. AD), Perspectiva. 73 Alhazen combined Greek mathematics with physical insights in how vision works: the form (‘sura’) of things passes into the eyes > brain, light radiates from every point of objects [in every direction] in straight lines, ingenious application of Ptolemy’s dioptrics – refraction of rays, concenctric curve of lens and cornea.
74 Robert Grosseteste, Roger Bacon and John Pecham linked mechanistic optical theories and linear perspective ( ) 75 Bacon: optics as model how God spreads his grace to the world (infusion of grace illustrated through the multiplication of light [metaphor]), so insight in optics leads to insight into the very nature of God – lux gratiae (St Antonine, Florence). Grosseteste about the nature of light: lux created the first day – basic force of divine energy, called ‘species’ (elementary energy, behaving according to geometrical and optical laws) – all objects emit ‘species’. 76 Bacon, De Multiplicatio Specierum: species have corporeal existence, they interact (species as forces going out of all objects as the sun, the eyes, God himself), bodies are interacting upon one another (cause and effect consciousness); 77 Pecham, Perspectiva communis (1265): review of Alhazen. Blasius of Parma, Questiones Perspectivae (1390); Toscanelli (1420), Della prospettiva.
80 Alberti wanted to write not as a mathematician but as a painter, because mathematics is about shapes and forms in the mind, divorced entirely from matter: ‘we talk of things that are visible’. Compare the concept ‘point’:
Leonardo Fibonacci (Practica Geometrica): id quod (abstract)
Alberti: signum quod (concrete, mark, like a dot on paper)
Albert was looking for concrete (physical) words for mathematical/optical abstracta, e.g. ‘horizon’ - A: ‘we will use a metaphorical [sic!] term from Latin and call it ‘brim’ [ora] or the ‘fringe’ [fimbria], this outline [in mathematics the edge [ambitus]] of a plane will be composed of one or more lines, 82 the ‘plane’ as composed of many lines, like threads in a cloth. From abstract to concrete – the poetry of the real (and artistic) life. Alberti also concrete about visual rays – fast between eye and the surface seen, Alberti imagined rays like extended very fine threads gathered together tightly in a bunch with in the center the ‘centric ray’ (the ‘prince of rays’). 84 rays loose sharpness over great distance through air [atmospheric perspective]. 85 the position of the centric ray and distance play a large part in the determination of sight, 86 cf Dante: ‘looking someone straight in the eye’. cf the straight avenue (street alone for the rich) that connects Castle Sant Angelo with St Peter’s in Rome:

88 Bacon: every quantity is infinitely divisible (cf Aristotle) > applied to the image (species) of a thing – as many parts as the object. A fundamental assumption of linear perspective is the proportionality of the object and its representation. A: paint in a picture not only what the eye sees, but also as the eye sees.
91v Ptolemy gave in his Geographia 3 methods to represent the known part of the globe (the oikumenia) on a plane. The third method was a carthographic method of linear perspective: the oikumene as seen from one vieuwpoint (mappamundi). 111 Ptolemy’s atlas arrived in Florence in 1400, just before the outburst of creativity, 114 this new approach provided mathematical unity for the geographic knowledge in a coordinate framework (grid-system). 118 A similar grid-system was applied in Alberti’s ‘velo’, a gridlike veil that organized the visible world into a geometric composition, structured on evenly spaced grid coordinates (De Pictura, Book Two): object ‘represented on the flat surface of the veil’. 120 Relation rediscovery of Ptolemy’s atlas, the rediscovery of linear perspective (Brunellesci) and the rediscovery of America (Columbus), 121 cf Toscanelli, writing to the Portugese court about sailing routes to the Orient.
125 Brunelleschi: idea of the perceptual [sic!] ‘truth’ of linear perspective.
Brunelleschi’s drawings of the Florentine baptistery (frontal and oblique) and the Palazzo Vecchio (oblique) were the first Renaissance perspective constructions. 128 Manetti: ‘It seemed as if the real thing was seen (..) I have seen it many times (..) so I can give testimony.’ 129 These two works of Brunelleschi showed a new geometric construction which could give a sense of unity and consistency to any illusionary picture, surpassing the familiar conventions [sic!] of naturalism. B was inspired by making scale drawings of architecture. 134 The flat lead-backed looking glass as mirror was introduced in the 13^th century > public and artists interested in mirrors [OBW flat planes] 135 Filarete: look in the mirror to see what you see with the naked eye. 152 Mirror in those days the metaphor for how vision ‘worked’ – crystalline lens as a kind of mirror in the eye.
Brunelleschi’s first work:
1 looking through the peephole of the painting in the mirror
2 removing the mirror and seeing the same
3 understand perspective and how seeing ‘works’
153 Erwin Panofsky: what is ‘seen’ is not visual reality, but a particular construction of pictorial space (culturally bound) – an artistic convention (which idea pleased modern artsts like impressionists and cubists). 154 This approach was defended by Rudolf Arnheim, Gyorgy Kepes and Nelson Goodman. Panofsky stated that the Greek ancients saw the visual world curved. Opposition from Gombrich, Gibson, ten Doesschate and Pirenne. 155 Panofsky derived his vision from Ernst Casimir’s symbolic forms (neo-Kantian idealism). 167 Words, images, myths take on their own ineluctable reality. This approach revived in ‘structuralism’. Panofsky: each historic period has its own special ‘perspective’ [sc Weltanschauung]:

antiquity: space as discontinuous residu between objects (not uniting them)
Aristotle: space is discontinuous and finite
late antiquity: space more world of spirits than of matter
christianity: space as ‘unifying fluid’ (represented by monochromatic gold or purple)
Romans: space and bodies compressed in patterns
Gothic: enclosing space around each figure (individual spaces)
Middle Ages: space is not homogeneous & uniform, everything has its proper place related to the center of the universe
14^th century: empirical space, allowing for factual observation of physical relations between objects
15^th century: systematic space, infinite, homogeneous, isotropic > advent of linear perspective

163 the Renaissance rediscovery: only that which is seen from one fixed viewpoint, can be represented on a flat surface according to precise geometrical rules which are derived from the science of optics.
164 Linear perspective pictures: anyone can learn [sic!] to become oriented or respond to linear perspective (cf children, ancient Chinese, Middle-Age christians and Arabs were not).
Coincidental: Gutenberg’s invention of movable type – both (linear perspective & movable type) more communication, widespread ideas with underlying mathematical harmony of nature.
notes
173 (from M.R. Cohen & I.E. Drabkin, A Source Book in Greek Science, 1948) Procus Diadochus (5^th century AD), commentator on Euclid, stating that optics is derived from geometry, taking lines as visual rays, using the angles formed by these lines. Division of optics in:

optics: illusions in the perception of objects at distance, e.g. the apparent convergence of parallel lines
catoptics: every kind of refection of light
scenographia: how objects at various distances and of various heights mayh be so represented in drawings that they will not appear out of proportion and distorted in shape

174 Alberti: metaphor of eye as ‘living mirror’, taken from Democritus in Aristotle’s De Sensu et Sensibile, II,438a)
187 Leonardo da Vinci: two visual pyramids – one with the apex in the eye and as base the horizon (the universe), one with the base in the eye and the apex on the horizon; the second springs from the first. [OBW visual systems represent the universe, pictures represent the visual and cultural systems, the interpretation of ambigeous scenes is also culture-driven by the observer’s psycho-social history].
192 Panofsky explains the fishbone perspective (with a cluster of centric points on the vertical centric line) by a convex or concave (curved) surface as seen – projected on the flat surface of a plane picture.
197 late 14^th, early 15^th century: as characteristic of the international style an active interest in naturalistic details; unifying geometrical linear perspective in ‘istoria’ as metaphor for God’s masterplan for the universe

Kheirandish, E., The Arabic Version of Euclid’s Optics (2 Volumes), 1999
The Arabic "translation" being both the Arabic version of the Euclidean text as well as the Arabic ‘version’ of the Eculidean visual theory. Euclid ca 300 BC.

Manuscript of an Arabic version of Euclid’s Optics, Universiteitsbibliotheek Leiden

In Vol.2 K compares the next texts of Euclid’s Optics:

Euclidis Optica (ed. Heiberg, Greek A
Opticorum recensio Theonis (ed. Heiberg, Greek O)
Kitab Uqlidis fi Ikhtilaf al-manazir (Arabic – 5 copies m1,m2,m3,m4,m5)
Tusi, Tahrir al-Manazir (Arabic ed. Hyderabad T)
Euclid, De visu (Arabic ed Theisen V)

Here below I quote some of Euclid’s definitions and propositions, of which several can be taken as demonstrations of different depth clues.
Definitions
1 The ray issues from the eye in straight lines while producing straight paths of infinite multitude.
2 The figure enclosed by the ray is a cone whose apex is next to the eye and whose base is next to the extremity of the visible object.
3 Objects upon which the ray falls are seen, and those upon which it does not fall are not seen.
4.1 That which is seen throug a large angle appears large;
4.2 That which is seen through a small angle appears small;
4.3 That which is seen through many angles appear more [clearly];
4.4. That which is seen through equal angles appears equal.
[ other versions have 7 definitions ]
Propositions [with the demonstrations (geometrical proofs, burhan) left out]
1 Nothing among visible objects is seen all at once.
[OBW the demonstration expresses an early formulation of the limited speed of light (rays)! Shorter rays = seen before, ‘although the object may be imagined to be seen all at once because of the speed of the sight’s glance’]
2 [Of] equal magnitudes unequally distant [from the eye], those closer [to the eye] are seen more accurately. [ OBW texture gradient ]
3 Every visible object has a limit of distance that once crossed is not seen. [OBW vanishing point? The demonstration suggests that ‘occlusion’ is meant. But in the margin of m1 and integrated in T the proof has been formulated in terms of the effect of the increasing distance on the decreasing size of the visual angle, sucessively expressed as becoming small (tasghuru), narrow (tadiqu) and vanished (ghaba), cf m1: ‘until it moves away until a limit’ V2, p 35]
4 When equal magnitudes are [placed] on the same line, the one toward which the path of the ray is the longest, is seen as the smallest.
5 Equal magnitudes unequally distant [from the eye] are seen as unequal, and the one closer to the eye is seen as the greatest. [OBW size constancy]
6 Parallel lines are seen from a distance as [being] unequal in width.
7 Parallel lines [on a plane] lower than [that of] they eye are seen from a vertical [distance] as unequal in width.
8 When equal magnitudes are placed on different locations [of the same line] they are seen as unequal in size.
9 [For] equal parallel magnitudes with locations unequally distant [from the eye], their difference of aspects is not seen according to the [ratio of the] magnitudes of their distances.
10 Right-angled figures, when seen from a [far] distance, are seen as circular. [OBW strange – I don’t see it]
11 [Of] planes below the eye, the most distant one is seen as the highest.
[OBW argued using a picture plane, sc HZ, see:]

12 [Of] planes higher than the eye, the most distant one is seen as lowest.
13 [Of] those magnitudes distant from the eye and facing it, those to the right are seen to the left and those to the left are seen to the right.
14 When equal magnitudes are below the eye on the same side, then the one that is [most] distant is seen as higher than the one beneath it.
15 [Of] equal magnitudes higher than the eye, that which is [most] distant is seen as the lowest.
[OBW I hold the combination of the propositions 3, 4, 6, 7 and 11-15 for a description and demonstration of linear perspective – taken together they imply vanishing points as well, which would also be the first one thinks of when reading proposition 3 ‘Every visible object has a limit of distance that once crossed is not seen’, despite its demonstration which seems to go in the direction of occlusion.
16 & 17 more clearly handle the phenomenon of occlusion, explaining the effect when the eye moves in such a way the the remote object hides more and more behind the object at closer distance.]
(..)
19 [What to do] when we wish to know a body’s height by means of the sun.
[OBW Euclid’s Optics is not only about appearance, but also about quantitative measurement. The proof starts with the next expression: ‘Let the body be AB and let the ray that issues from the sun be GD’. In this proposition also the luminous rays from the sun are reduced to rectalinearity as geometrical property. The following calculation (tracing back to Thales) uses the ratio – unknown body AB : known body EZ = known distance BD : known distance ED in order to determine the magnituted of AB:]

23 If a circle is placed in the same plane as the eye, the circumference of the circle appears to be a straight line (it’s difficult to detect curvature (convexity or concavity), especially from a greater distance).

26 When a sphere is seen by both eyes, and the distance between the eyes is equal to the sphere’s diameter, then that which is seen of the sphere is half of it entirely. [OBW stereopsis, together with 27 (smaller sphere - convergence) & 28 (larger sphere)]

[OBW other propositions explore the relative sizes of moving objects, or the effects of a moving eye on the perception of objects with equal magnitudes in different positions]

[OBW also elegant analyses of perceiving unequal magnitudes as equal, e.g. 54,55:]

61 When the eye is moving, distant objects are thought to be different [in speed] from those closer. [ OBW motion paralax ]

visual rays from or to the eye
Theisen (1971, 30):
Pythagoreans: visual rays emitted from the eye
Epicureans: the eye receives impressions from the object
Democritus: object > images in the air > transmitted to the eye
Plato: visual rays + sunlight (Temaeus)
Th: Euclid most probably visual ray theory from the eye, cf 1^st proposition ‘rays sweeping over the object’)
Th (275ff) argument from density of rays: details or small objects are not seen

artificial and perceptual perspective
Theisen (1971, 287ff):
Artificial perspective is essentially a mathematical way of constructing space on a flat surface and at the same time achieving a pictorial unity (..) based on two assumptions: 1. we see with one eye which is stationary, 2. projection of objects onto a plane cutting across the visual pyramid gives an adequate representation of what is seen [space homogeneous, infinite, stable, isotropic]
[OBW Perceptive, natural perspective has more (different) properties.]

Kubovy, M., The psychology of Perspective and Renaissance Art, 1986
6 Renaissance linear perspective is a new code for concealing meaning (illusionistic, narrative, structural focus). 16 Renaissance painters created a deliberate discrepancy between the spectator’s actual point of view and the point of view from which the scene is felt to be viewed. 28 plan (view from above), elevation (view from the side) 30 use the elevation to draw the eye-line, use the plan to determine the vanishing points and the front view of the object(s) and connect the front points to the vanishing points:

37 Brunelleschi was the first who painted intuitively perspective representations on panels which had to be viewed through a small peep-hole in the centre of the panel in a mirror in order to provide the illusion of depth. There is no substantial evicence that he understood the underlying geometrical theory.
40 Stereopsis is only effective within the range of a few yards (cf threading a needle using one or two eyes). 43 Seeing vivid depth within 200 cm is contradicted by seeing the surface of the picture-plane and its flatness, opposing the impression of depth suggested by the picture. Wall- and ceiling-paintings (like Porro’s ceiling fresco (1694) in the Church of St Ignazio in Rome [OBW pictorial illusion of open heaven as religious illusion]) are distant enough.

[OBW also the corner of view plays a role in order to support the effect of pictorial illusion, see e.g. the two seemingly identical churches that had to be build at the Piazza del Popolo in Rome, but on different pieces of ground, for which the dome on the smaller piece of land had to be made elleptical (pictures made in May 2007)]

47 A smaller apperture size of the lens (or pupil in the eye) yields a greater field depth – cf the small peep-holes in the ‘perspektyfkas’ of e.g. S. van Hoogstraten (1627-1678) which reduces the size of the pupil (‘artificial pupil’) in order to increase the depth of field and by that enhancing pictorial depth, also reducing information about the flatness of the painting by trunctating the visual field by ‘removing’ the immediate foreground, picture margin and nose. 67 Emmert’s law: the apparent size of the object you see when you experience an afterimage, is directly proportional to the perceived distance of the surface at which you are looking. 89 The robustness of perspective suggests that the visual system infers the correct location of the center of projection. 99v The bounds of perspective are related to the amount of distorsion, e.g. only forks (3 angles > 90 degrees) and arrows (2 angles < 90 degrees) are perceived as vertex of a cube. Another example: a visual angle of 102 degrees from the center of projection is perceived as distorted to all viewers except from a distance of one inch, which is too close to be able to focus on the lines:

The visual field which yields a ‘perspective normale’ (Olmer, 1943, 1949) is 37 degrees horizontal and 28 degrees vertical, which can be seen in the cube-pictures Olmer provides:

and which is confirmed in several experiments (e.g. Sander 1963, Kosslyn 1978, Finke & Kurtzman 1981) 111 Perkin’s laws (regarding forks and arrows) suggest that what we perceive as distorted, just captures the deviations from what we are accustomed to see.
113ff Examples of the primacy of perception over geometry
The next picture shows that the central projection of a sphere not on principal ray is an ellipse and does not look like a sphere:

But have a look at Raphael’s The School of Athens (1511):

and have a closer look on the spheres on the right side of this painting:

It seems that only circles are considered to be acceptable pictorial projections of spheres.

Another example of the primacy of perception over geometry is the way artists paint a series of columns. Leonardo da Vinci remarks that the further the columns are from the principal ray, the wider the projected diameters of the columns and the smaller the ‘room’ between the columns:

Looking through a peep-hole at the center of projection this would have the right effect, but in order to provide a ‘natural look’ as perceived by different viewers from different angels the columns have to be painted in equally wide projection.

116 Also the artists never complied with the implications of geometry for e.g. the representations of human bodies. 117 Which often implicated the use of different perspectives in one picture, as can be seen e.g. in Paolo Uccello’s Sir John Hawkwood (1436):

Here we find several viewpoints in a single composition: a low viewpoint for the architecture and a high viewpoint for the rider & horse.
121 So we find as convention of painting the primacy of perception, which implies that architectural elements are painted according to central projection, where other bodies are drawn by size and position, but then each body drawn from a center of projection on a line perpendicular to the picture plane, intersecting the picture at a point inside the contour of the body. Which means that Renaissance perspective is not geometrically rigid, but flexible, subtle and complex.
125 The laws of perspective do not coincide with the geometry of central projection. In two ways the practice of perspective drawing deviates from central projection: 1. the restriction of the perspective pictures to 35 by 28 degrees, 2. the representation of round bodies (spheres, cilinders, human figures etc) as if the principal ray of the picture ran through them – in order to avoid marginal distortions.

150v There can be a kind of separation of the body’s eye and the mind’s eye (the disembodied eye, the movable egocenter), which can occupy a virtual point of view (cf looking at a movie). Leonardo da Vinci appealed to this flexibility of virtual point of view while painting The Last Supper (1498):

Some elements of this picture look distorted when looked at from the groundfloor of the Church:

Analysis of the perspective construction yields the next pictures:

The center of projection is at a distance of 10.075 m and a heigth of 4.6 m above today’s floor. Seen from this center of projection it can be perceived that Leonardo continued the walls in his fresco, which look distorted from the ground below.

Kubovy concludes (148): Leonardo elevates the viewer to a higher center of projection, thus achieving a feeling of spiritual elevation.

163 Panofsky (1927) argued that each historical period has its own special ‘perspective’, reflecting a particular ‘Weltanschauung’, wich opposes the radical relativistic conventionalism Goodman (1976) et al. represent. 165 Linear perspective is a geometrical system, tempered by what perception can or cannot do – a system adapted to the capabilities of our perceptual system (cf Welch, 1978). We cannot arbitrarily change the way we perceive. 169 Gablik (1976) argued that Renaissance presents a deterministic world-picture, which orders the universe in terms of geometry, yielding a one-point-perspective (nature as a vast geometrical system, fixed world, absolute space & time, no chance or indeterminacy). 170 Kubovy regards this is a caricature of Renaissance Art, in which geometry always was subordinate to perception, using perspective to free oneself from one’s special (egocentric) vantage point.

Theissen, W.R., The medieval tradition of Euclid’s Optics, 1971
Different versions of the book Optics contain more or less assumptions, like e.g. 7. more rays (..) are seen more clearly, 8. all visual rays have the same speed, 9 an object is not visible under every ray whatsoever, leading to e.g. prop. 1 Nothing that is seen, is seen at once in its entirety. (47 8 and 9 are not in the Greek, only in the Latin text)

12 Two Latin translations have as title ‘Perspectiva’ (equivalent with the Greek ‘Optica’). Different Arab translations were made in Spain by the Saracens.
24 Aristotle in Physics II,2: ‘optics investigates mathematical lines qua physical’.
25 Euclid’s propositions 6,7,11,12,13 et al are ‘all closely related to the notion of a vanishing point or line’.
26 Richter (1965): not one point of view, one space, one light until Renaissance.
27 1^st century BC Geminus: ‘convergence of parallel lines’ as illusion in the perspective of objects at a distance (taken from Proclus’ commentary on Euclid’s Elements).
30 Euclid’s Optics has two main assumptions: the rectalinear visual rays and the the visual cone (location/orientation) as physical realities.
35 T Euclid most probably visual rays as emitted from the eye [extramission theory] (cf prop. 1: rays sweeping over the object).
36 Euclid assumes rectalinearity of the rays and the cone properties, in order to be able to write a geometrical treatise.
38 Euclid did not limit himself to perspective – several propositions were concerned with more than appearances. Optics is also measurement in order to determine the absolute size of objects, cf the quantitative steps e.g. in propositions 19-22. 45 E dealt with appearant relative size and absolute size.
51 T: Euclid’s Optics lacks the rigor of the Elements [in its proofs].
275 Euclid seemed to regards rays as discontinuous. He used the fact that one does not discern some details of small objects as argument against the theory that rays go from the objects to the eye [intromission theory].
287 Artificial perspective is essentialy a mathematical way of constructing space on a flat surface and at the same time achieving a pictorial unity (..) based on two assumptions:

we see with one eye that is stationary
projection of objects onto a plane cutting across the visual pyramid gives an adequate presentation of what is seen

This artifical perspective (homogeneous space, constructed, infinite, stable, isotropic) is different from the natural (perceptive) perspective.
The geometrical space is different from the space of perception.

$$$

For instance Arnheim (1974), Goodman (1976), Wartowsky (1978), Hagen (1986) and Hudson () argue that linear perspective is a matter of convention.
Gombrich (1969,1982), (..) Derksen (1999, 2001, 2004, 2005) argue that linear perspective is a matter of geometrical and perceptual necessity.

Abstracts in het Nederlands

J.H. van den Berg (1914), historisch fenomenologisch realist
De historiciteit van de veranderingen moet niet alleen in haar eenvoudige chronologie worden bestudeerd, maar ook situationeel in haar synchronie (gelijktijdigheid).
De veranderingen bepalen het perspectief van de waarnemingen, met als gevolg dat de mensen zich anders in de wereld gaan oriënteren.
Fenomenen: feiten, gebeurtenissen, ervaringsgegevens.
Metabletica: onderzoek naar het fenomeen van het synchroon veranderen van de relatie tussen de dingen en de mensen (uitgaande van de veranderlijkheid van de dingen en de intentionaliteit van het menselijk bewustzijn).

Onderzoeksvraag: welke fenomenen in een bepaalde tijdsperiode behoren tot de zaak zelf van de verandering? Daarbij oog voor de samenhangen van min of meer gelijktijdige veranderingen op verschillende gebieden (zoals bv wetenschappen (buiten) kerk-architectuur (grens), spiritualiteit (binnen)).
Wat verandert er nu eigenlijk: het menselijk inzicht in iets dat altijd al zo was of zijn de dingen zelf veranderd en neemt de mens dat slechts waar? Of is de verhouding van een mens en de dingen om hem heen zo intiem dat we moeten aannemen dat beide, zowel de mens met zijn inzicht als de dingen in hun materialiteit, veranderen?
Verbanden tussen synchrone veranderingen bepalen de betekenis van die veranderingen en hun gevolgen.
Lezingen (Delft1993, op de metabletica website gezet als smaakmakers), samenvatting:
1
Hoe dingen veranderen.
Verandert kunst de natuur (Wilde)?
Hoeveel tijd bezit de echte roos tov een kunstroos?
( Roos typisch Europese boem – cf Japan: kersebloesem (teer aan de tak))
Hoeveel tijd bezit een steen – tijdloosheid; omkeren: fossiel ammoniet (Mesozoïcum, 100 miljoen jaar geleden) – oertijd; ander stuk steen omgekeerd: reliëf uit de tijd van de neogotische architectuur – 1800 – tijd aangebracht in tijdloze steen.
Verschillende betekenissen van tijd uitgewerkt in verschillende verhoudingen van verleden – nu – toekomst.
a. tijd alleen als ‘nu’
Voor defect-schizofrenen bestaat wel de objectieve tijd (kloktijd nu, jaargetijde nu), maar niet de ‘geleefde tijd’ (Bergson: temps vécu): ‘de bladeren vallen niet meer’ (herfst niet te herinneren), ‘klok is geen tijd’ (de klok loopt niet). In zo’n wereld zonder tijd gaan de verbanden verloren, waardoor de defect-schizofreen aangewezen is op noodverbanden (hallicunaties en wanen).
b. tijd alleen als ‘verleden’
1619 Descartes. Ontdekking van een eenvoudig [en al eerder bekend] principe als principe dat (ook) geldt voor de natuur: wanneer men van een wiskundige reeks twee of drie [beter: een beperkt aantal] termen kent, zijn de daarop volgende termen gemakkelijk te vinden. door vdB vertaald als: in de natuurwetenschappen zijn alle dingen dingen met een tijd tot nu toe (voldoende verleden om de toekomst mee te kunnen voorspellen). Basis voor de moderne geneeskunde en techniek, bv 1628 Harvey: publicatie over hart (als pomp) en bloed.

Aristoteles: causae efficiens (teweegbrengende oorzaken), causae finalis (doeloorzaken, in de theologische dogmatiek toegepast op Gods doel met de schepping). Sinds Descartes geen geloof meer in ‘doeloorzaken’ (in concurrerende theologische dogmatiek te gebruiken voor een schepping uitsluitend als resultaat van Gods wil).
c. tijd als voortgang van verleden naar toekomst, waarbij het ‘nu’ voorzien is van dingen met verleden en toekomst (leven/beleving van de gezonde mens)
d. tijd als toekomst die het ‘nu’ overweldigt: wonderen (in een wereld met verleden dingen komen geen wonderen voor), voorbeelden: verliefdheid, inspirerend onderwijs. [OBW toekomende tijden als ongekende (irreducible and unpredictable) mogelijkheden]
2
Machines
1773 John Kay eerste weefmachine > spinmachine > betere weefmachine > betere spinmachine etc. vdB: de samenleving op hol, n vakmannen > (n-w arbeiders + w werkelozen)
1776 Adam Smith - The nature and causes of the wealth of nations, vergroting van arbeidsproductiviteit door arbeidsdeling
samenhangen:
1740 Trembley: deling van de zoetwaterpolliep (deling is vermenigvuldiging)
1740 Richardson, roman met ‘sentimental analysis’ ((in)deling van gevoelens)
Zonder distantie geen deling: er is klaarblijkelijk een zekere distantie opgetreden, daar in het begin van de 18^e eeuw, tussen mens en omgeving, tussen mens en medemens, mens en stof en die distantie is verantwoordelijk voor een nieuw proces in de biologie, voor een nieuwe beschouwing van de medemens en voor de industriële revolutie, voor de deling van de arbeid. (..) En die distantie komt omdat onze godsdienstige instelling toen is veranderd. vdB: naar mijn vaste overtuiging is deze centrale instelling ten aanzien van de geloofsleer verantwoordelijk in laatste instantie voor de verandering in de natuur, voor de verandering in de relatie mens tot medemens en ook voor de industriële revolutie. [OBW vroeger ging bij vdB het ‘buiten’ voorop] (..) Gevolg: vervreemding, niet alleen van het ambacht (Marx), maar van de hele intimiteit met mensen, dorp, stad en wereld.
Ook goede effecten. De machine heeft het leven van de goede arbeider (die ‘t werk hield) verbeterd, de adel en de geestelijkheid vernietigd en maakte in die zin een samenleving die eerlijker was (loon naar werken), ook al mist hij nog veel. [OBW winst van een sociaal-liberale democratie: juridische gelijkheid als uitgangspunt voor het liberaal kunnen en mogen ontstaan van sociaal-economische ongelijkheid op basis van verdienste, waarbij uitwassen in verdiensten sociaal worden ingetoomd ten bate van het in stand houden van een vitale samenleving, waar juridische gelijkheid etc. (feedback-loop) Het menselijk lichaam als metafoor voor de samenleving: noodzaak van het vitaal blijven van elk deel van ‘t lichaam. Waar geen doorbloeding meer is (bloedgeld), rotting en dood.]
3
Gelijkzwevende stemming en differentiaalrekening
Begin 18e eeuw: Bach ‘Wohltemperierte Klavier’, door aanpassing van de piano (gelijkzwevende stemming zodat alle akkoorden in elke grondtoon harmonisch kunnen klinken) mogelijk om stukken te spelen in alle toonsoorten.
consonanten (terts, kwart, kwint), dissonanten (bv twee toetsen naast elkaar)
Werckmeister heeft de ‘huilende wolf’ over alle kwinten uitgestreken en van één grote valsheid een serie kleine valsheidjes gemaakt. Sinds deze stemming is alle muziek een beetje vals. vdB samenhang gelijkheidsdenken (Locke) > democratie. Max Planck: componeren in de reine stemming zou wel weer kunnen (vdB weet niet hoe – wel dat er dan beperkingen zijn in het componeren – cf beperkingen in het omgaan van mensen met elkaar).
Mercator: orthogonale hyperbool in formule y = 1 / (1 + x) = 1 - x + x² - x³ + ...
waarmee hij rust in ‘beweging’ veranderde, waardoor je macht krijgt over wiskundige eenheden die je anders nooit kunt bepalen.
Brounckner maakte van deze reeks een logaritmische reeks:
log (1 + a) = a - 1/2 a²+ 1/3 a³ - 1/4 a⁴ + ...
Berkeley had grote bezwaren tegen het principe van de differentiaalrekening. Hij merkte op dat de differentiaalrekening, die zoveel successen boekte, te maken had met ghosts of departed quantities. (vgl de eerste crisis in de wiskunde: de onmeetbaarheid van Ö 2 in de stelling van Pythagoras), vgl ook de wiskunde-kritiek van de intuïtionist Brouwer.
Maar je kunt in de mechanica, fysica en technologie prima uit de voeten met de differentiaalrekening.
vdB het wringt niet in de toepassing, maar misschien wel in het effect (van kogelbaan naar kernbom).
synchronische samenhangen:
Perault (Parijs, schrijver eerste sprookjesboek die het kind kinderlijk maakte door het af te schrikken van de ‘volwassen wereld’): wij weten het beter dan de kassieken.
Locke steekt de draak met erfelijkheid – alle kinderen bij geboorte gelijk, de mens kan zich vrij bewegen, vs goddelijk recht van het koningschap;
ontwikkeling van stabiliteit naar dynamiek.
4
Wat verandert: mens of materie?
De werkelijkheid verandert voortdurend.
1316 Mundinus, anatomisch boek voornamelijk gebaseerd op sectie van dieren en dus met veel foute afbeeldingen voor zover deze zouden moeten gelden voor de menselijke anatomie.

1543 Versalius – keek wel naar de anatomie van mensen > beter boek
[1543 Copernicus – niet de aarde, maar de zon als middelpunt]
vdB: wij vandaag een grote brei van ongeloof die het bemoeilijkt om de religieuze wereld van de middeleeuwen te ‘zien’
Voor de tijd van Harvey (1628) konden medici het hart niet ‘horen’ kloppen.
vdB verschillende waarden van het landschap (waar goede en kwade goden huizen) werken door in het ontstaan van godsdienst, eredienst (goden controleren), Grieken/Romeinen: tempel naar buiten gekeerd (goden in het landschap, vertegenwoordigd in de tempel die contact met het landschap blijft houden), christendom: kerk naar binnen gekeerd (god in hemel en vertegenwoordigd binnen de kerk)
vdB: Zo gauw de geloofsleer gaat veranderen, verandert de kerkbouw en ook de natuurwetenschappen. [OBW In Metabetica van de Materie I staan de veranderingen in het ‘buiten’ nog voorop – wat onduidelijk hoe strict de synchroniciteit van de veranderingen bij vdB werkt]
Bij de Grieken geen natuurwetenschap en techniek, bij de Christenen na de ontgoddelijking van de natuur (na 1000) wel. [OBW vanaf 1000 god trekt zich terug (landschap>kerk>innerlijk) – Nietzsche: god is dood – vdB na 1900 weer tot leven gewekt?]
Einde 18e eeuw, vlak voor de Franse Revolutie:
Lavoisier: water geen element, maar deelbaar (H₂O, deelbaar in waterstof in zuurstof, democratisch water: alle water één pot nat, geen verschil meer tussen een beekje en de Zuidzee)
Goethe: dubbelganger, meervoudig ik, later Freud: ich, ueberich, onbewuste.
vdB Wat verandert, is de samenhang van mens en wereld.
Zonder betekenisgevend mens is de wereld niets, een leegte.
De betekenis verandert, neemt telkens andere gedaantes aan, zonder aanspraak op ‘de waarheid’.
(..)
waarnemen is nog niet zien (inzicht)
Voor meer details van vdB’s metabletische constructie, zie bij de abstracts op de volgende pagina

Het voorgaande kan dienen als achtergrondinfo bij de gedachten van vdB over lineair perspectief en de niet-Euklidische meetkunde, die door hem wordt uitgelegd als projectieve meetkunde op de lijn van het perspectief (Metabletica van de Materie, I, Meetkundige beschouwingen, 1968).
306v De ontdekking van centraal perspectief (1420 Brunelleschi, 1435 Alberti, ‘construzione legitima’) wordt voorafgegaan door de herontdekking van de klassieken vanaf 1000 en hangt samen met de migratie, de plaatsverandering van god (uit het buiten van de mensen weg naar het binnen van de mensen toe (verinnerlijking)). Een volgens strikt lineair perspectief getekend beeld is levenloos, want wij zien bij gratie van bewegende ogen en bewegende objecten. [OBW > combinatie van nabeelden] Strikt perspectief werd dan ook niet toegepast door de kunstenaars (dichterlijke vrijheden). Met de Romaanse bouwstijl (afsluitend binnen) werd het buiten vrijgegeven en kon de westerse natuurwetenschappelijke instelling ontstaan. Met de Renaissance-tempel (die meer open naar buiten lijkt) breekt echter niet een nieuwe sacralisering van het buiten aan. Het lineair perspectief bezet het buiten volledig met punten en lijnen zodat er een einde komt aan een ‘open’ wereld met overal plaats voor god. [OBW Een wereld zonder metafysische valkuilen is vrijmoediger te onderzoeken.]
[geschiedenis van de afstanden: tot 1740 onbereikbaar ver (eindig hemelgewelf), 1740 – 1900 oneindig (?), na 1900 weer onbereikbaar ver (onbegrensd eindig heelal) daarmee samenhangend: 1000-1740 kerkbouw tot 1740 steeds hoger, verinnerlijkende spiritualiteit,1740-1900 neo-stijlen: men weet ‘t niet meer, leeg innerlijk, na 1900 humanocentrische spiritualiteit
pg 386 vooropgaan van het buiten omdat het buiten primair is in ons leven – aarde als primordium
pg 396 materiële verandering van de relatie van mens en stof (leven in meervoud)]
1740 eerste aanzetten niet-Euklidische geometrie
1854 Riemann (drievoudige menigvuldigheid – manifold), 1870 Klein: verband materie en ruimtekromming > verschil oneindig en onbegrensd
pg 406v De lijn van het perspectief is metrisch te maken door exponentiële of logaritmische benadering (Cayley 1859). Op een enkele [perspectivisch getekende] rechte met het doorgangspunt O en het verdwijnpunt P is de niet-Euklidische hyperbolische meetkunde (van de scherpe hoek) gerealiseerd. Wanneer het imaginair getal Ö -1 wordt ingevoerd voor de afstanden die het oneindig gemaakte ‘doorgangspunt’ O overbruggen, is de niet-Euklidische [hyperspherische] meetkunde (van de stompe hoek) gerealiseerd.
De Euklidische meetkunde (van de rechte hoek) is het grensgeval tussen de vele meetkunden van de stompe en scherpe hoek.
417v samenhangen: ttv periode 1740-1900 beveiligingen tegen de oneindigheid: 1854 dogma van de onbevlekte ontvangenis van Maria, 1870 dogma van de pauselijke onfeilbaarheid ex cathedra; 428 associaties scherpe hoek met de eenzame mens in een oneindige ruimte, stompe hoek met de menselijke relaties, samen in een eindige wereld. rechte hoek: alleen in een naar één richting oneindige ruimte (Euklidisch, toen god er was, kon de mens alleen zijn). Na 1900 samen zijn zonder god in een gesloten wereld. 435 psychotherapeutische sprong vdB: mijn patienten willen dat hun onbereikbaarheid opgeheven wordt – relaties vermenigvuldigen met Ö -1.
Verander van plaats [voor een ander perspectief].

Does this picture of Giovanni Battista Piranesi (called ‘carceri’, around 1744) represent being locked-up in a non-Euklidian, finite but unbounded space (cf Vogt-Göknil, 1958)?

[OBW relatie waarneming, schaal en (niet-)Euklidische ruimte]
[wat kan de golflengte van licht beïnvloeden – ivm interpretatie van astronomische waarnemingen]
[equivalentie – doorgaande gelijkmaking, electriciteit en magnitisme, versnelling en gravitatie, … ]
[wanneer een ontdekking gedaan is - wanneer deze ontdekking leidt tot cultureel invloedrijke uitvindingen]

Notes OBW

Some of Euclid’s theorems, taken together, seem to point at and end in vanishing points on the eye-line:
Theorem 10 Of planes lying below the eye, the farther parts appear higher.
Theorem 11 Of planes lying above the eye, the farther parts appear lower.
Theorem 12 Of lines which extend forward, those on the right seem to swerve to the left, and those on the left to the right.
In the artistical practice one finds in most pictures that show something like linear perspective at most (what Panofsky, 1927 called) a fishbone-perspective.
Still I find it hard to belief that the ancient Greek did not connect linear perspective with different vanishing points on the eye-line. They were often enough at the sea-coast looking at the visual effect of ships sailing in different directions:

Taken the outlines of every ship as a circle, what is ‘drawn’ around the disappearing ships are just again ‘visual’ cones, which could be called ‘size constancy cones’, but now every cone with its apex in its vanishing point at the horizon which coincides with the eye-line when the observer is looking at the dissappearing ships.

Linear perspective can be a clue for size and distance of two identical copies of an object, but it’s not always clear which depth clues dominate the interpretation of the picture, as the next examples show:

Greek temples were designed with deliberate distortions to make the building appear correctly. Columns were given entasis, a slight swelling (convexity) in the middle, so they would look straight (sc compensate for the illusion of concavity created by parallel lines), and architraves were cambered up slightly in the center so they would appear straight, compare the Parthenon Columns.

During the Renaissance, European artists began to paint with the goal of greater realism. They learned to paint lifelike images and they became skilled at creating the illusion of depth and distance by using the techniques of linear perspective.

Consistent application of linear perspective unifies the picture – focal reduction to one point of view?

Cubism (1907-1914) the object is seen and pictured from different points of view by projecting images on top of each other (Braque, Gris, Léger) (influence of the changing space-time conception – Einstein, 1905?)

The position of our horizontal horizon in our visual field is determined by the height of our eyes. What is the position of our vertical horizon (the one on which one can find the vanishing points of high vertical buildings)? Compare:

Experienced graphical artists see the cathedral as in the picture above, but a lot of people see the cathedral as in the next picture:

What does this difference in seeing say about the (non-)conventionality of our vertical-perspective vision?

Compare the way Monet (and others) painted the Rouan cathedral:

with some pictures of this cathedral:

Vanishing points at another position (in this example point K) than the horizontal eye-line were used e.g. in geometrical arguments for reverse perspective: reconstructing the point of view, e.g. by Brook Taylor in 1719:

Rembrandt did master depth but did not (often) mind linear perspective.

In order to see see optimal depth in a painting (or photo): look from the focal point with one eye and limit the visual field to an area within the picture-frame: to be in the picture.

reverse perspective
Edgerton, 1975, p 199 (glossary): one must presume it a natural condition of seeing – objects giving more information when its sides diverge
but also: split-view (seeing more sides than would be possible from one viewpoint) is charateristic for children and primitive societies.
[OBW multiple viewpoints while moving & relation holography]

curvelinear perspective
what is very close, very far and around us, appears to be curved
Termes, D., New Perspective Systems, 2007
http://www.termespheres.com/perspective.html
On this page you can find the next illustrations and explanations of one .. six point perpective, where the curves come into play from the four point perspective on:

Especially of the the six point perspective works of art you can find nice examples, made by Dick Termes. His works of art generate a special type of optical illustion, called the Termes Perspective-Flip, which is of course only poorly represented by a 2D flat picture like the next one:

This example shows a transparent, black and white reproduction, 8" diameter sphere that shows the interior space of the St. Peter’s Cathedral in Rome. A remarkable illusion happens when this transparent sphere spins. You find yourself inside the sphere looking at the back side of the sphere, seeing the total building turn in front of you. It is as if you are actually standing inside St. Peter's turning in a circle - the front side of the sphere totally disappears. This transparent sphere is very difficult to photograph. What you see here is one hemisphere of the sphere. The camera just doesn't work like your eye and mind.
For other impressive examples, see:
http://www.termespheres.com/termesphere-movie.html
And especially for the ‘inside the sphere’ or ‘outside the sphere’ illusions, see:
http://www.termespheres.com/qt-directory.html
literature: Dick Termes, New Perspective Systems, 2007

Other examples of curvelinear pictures, taken with a fish-eye lens:

another lens, another view – evolution of lenses
compare other animal’s eyes [TODO]
elements of a camera [TODO] A camera makes the picture with the ‘right perspective’ if one takes the position of a ‘one-viewpoint-perception’, or are there ‘western’ and ‘non-western’ camera’s?
Which view more optimal in automated systems? E.g. fish-eye lens more info, spherical lens even more > interpretation of curvelinear images.

rectalinear perspective (easier to mathematize, functional distorsion of the curvelinear world?) as borderline-case of curvelinear perspective? linear perspective as (single?) calculable depth clue (combining geometry with a metrical system)? Distances also without metrical system judged well by the visual system – cf hunting skills (throwing stones, shooting arrows etc > focus target, curved trajectory)

If the picture is fixed (made static), there is most of the time only one point of view (in order to have the best view e.g. related to depth clues). This can be generalized to other fields, e.g. one fixed worldview or religion calls for a static point of view of the believer.

A single viewpoint representation does often not show the most significant properties of an eventity – a holographic representation shows more, involving a range of viewpoints and observed by moving.

A dynamic perspective on a continuously changing life and world can best be characterized by the movement through different points of view.

In several art-historical books can be found an in history often repeated pattern of movement through different points of view: 1. search of form (primitive stage), 2. becoming of form (archaic stage), 3 stability of form (classical stage) 4 deterioration of form (baroque stage).

Wat de gelijkzwevende stemming in de muziek doet, doet het variabele [multi-focale] perspectief in de beeldende kunst. Meerdere onderdelen perspectivisch een beetje fout maakt de voorstelling, die als geheel gezien wordt vanuit verschillende gezichtspunten, tamelijk goed.

skhnografia evoces drama, as Ankersmit has proven with his influence on the liberal party in the Netherlands, loosing the elections of 2006, partly due to their eager to show the dance of different points of view, which Dutch voters by that time liked between parties, but not within one party.